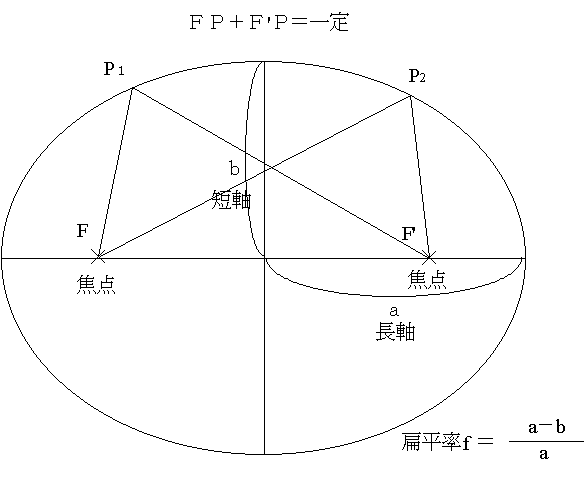
2定点（F、F'）からの距離の和が一定であるような図形をだ円（楕円）という。そのとき、この二つの定点を焦点という。
※ だ円については別の定義の仕方もある。また、だ円は円錐を切ったときに現れる図形でもある。円錐を切ると、円、だ円、放物線、双曲線が現れる。これらをまとめて円錐曲線という。
長い方の軸の長さ（ａ）、短い方の軸の長さ（ｂ）とすると、だ円の形（つぶれ方）は扁平率（扁率）（ｆ＝（ａ−ｂ）/ａ）で表わすことができる。ａ＝ｂならば円であり、このときはｆ＝0となる。また、ａ>>ｂ（ａがｂの対して非常に大きい）のときは大変につぶれただ円ということになる。ｂが無視できればｆ＝1。つまり だ円では、0＜ｆ＜１ で、ｆの値が0に近いほど円に近いだ円、1に近いほどつぶれただ円ということになる。
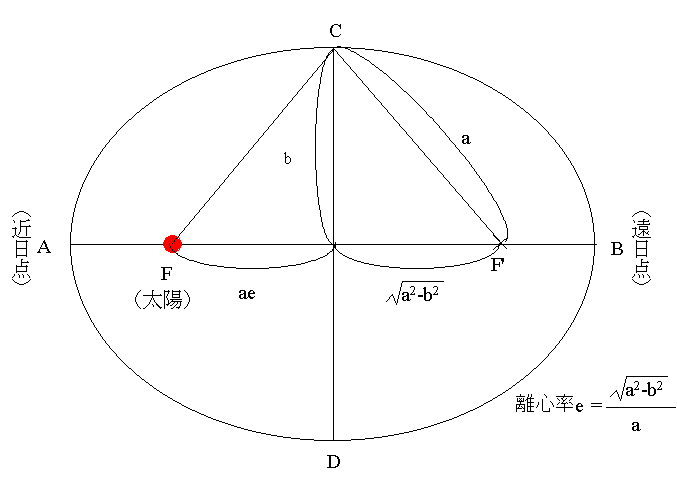
だ円が与えられたとき、焦点の位置はどのように求めるのだろう。いまだ円上の任意の点までの和が一定なのだから、下図でFB＋F'B＝FC＋F'C。ここで、だ円は軸に対して対象だから、F'B＝FA。つまりFB＋F'B＝FB＋FA＝２ａ。これはFC＋F'Cに等しい。FC＝F'Cだから、FC＝F'C＝ａ。
つまり、Ｃからａの距離に焦点がある。中心からの距離は三平方の定理（ピタゴラスの定理）より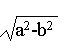
となる。 このとき、長軸（長半径）ａに対するこの距離の比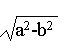（/ａ）を離心率（ｅ）という。離心率を使うと、中心から焦点までの距離は
ａｅ となる。また、近日点距離はa(1-e)、遠日点距離はa(1+e）となる。また、近日点距離と遠日点距離の平均はちょうどａになる。だから、太陽と惑星の平均距離は長軸の長さになる。
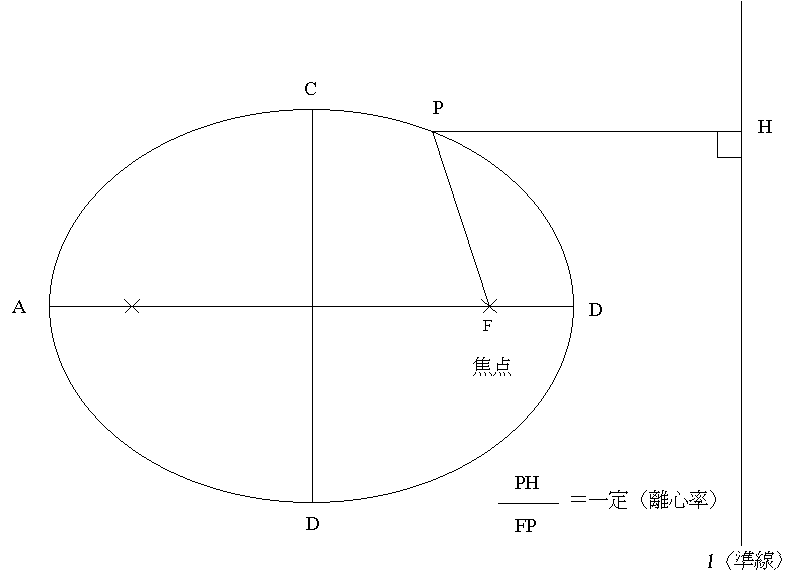
もう一つのだ円の定義：ある定点（Ｆ）とある直線（l）からの距離の比が一定（FP/FH＝一定）というものである。このとき、この比の値が離心率（ｅ）になる。このとき、この直線（l）を準線という。
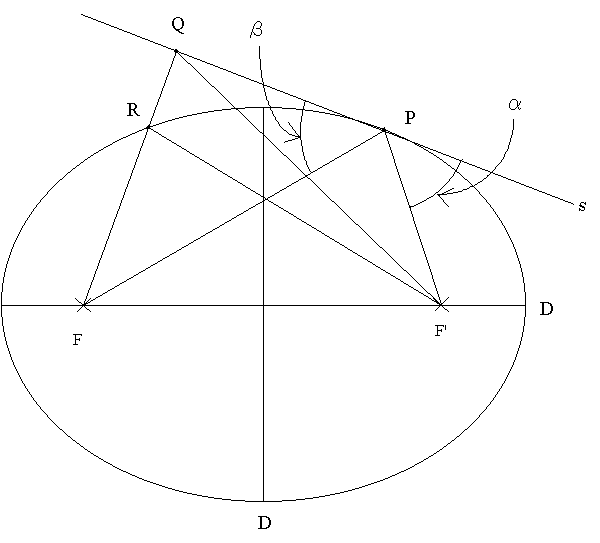
焦点：なぜFやF'焦点というのだろう。下の図で、だ円上の任意の点Pを考える。その点における接線（s）上の別の点Qを考えて、FP＋F'Pと長さを比較する。FQとだ円の交点をRとすると
FQ＋F'Q＞FR＋F'R＝FP＋F'P
つまり、s上の点を考えるとFからF'にいたる距離はPで最小になる。これは光の反射と同じだから、∠α＝∠β。つまり、片方の焦点から出た光は、だ円状で反射すると、必ず別な焦点を通ることになる。
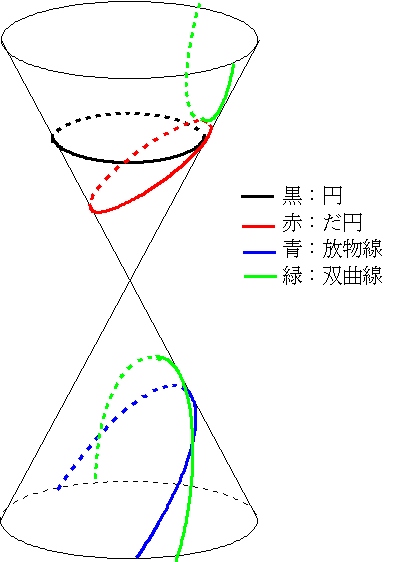
円錐曲線：下図のような円錐を考える。底面に平行に切った切り口が円、切り口が母線に平行になったときが放物線、母線よりも小さな傾きで切ったときがだ円、母線よりも大きな傾きで切ったとき（上下の円錐とも切ったとき）が双曲線になる。離心率（ｅ）で考えると、ｅ＝0が円、0＜ｅ＜1がだ円、ｅ＝1が放物線、ｅ＞1が双曲線となる。
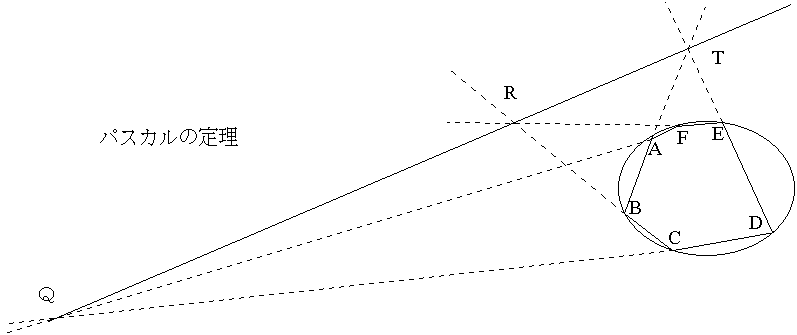
円錐曲線には共通する性質がある。例えばパスカルの定理。
パスカルの定理：円錐曲線に内接する6角形の対応するそれぞれ二辺（の延長の）交点は一直線上にある。下図ではだ円で示したが、円、放物線、双曲線どれでもよい。パスカル（フランス、1623年〜1662年）が16歳の時に考えて証明したという。
図ではAB-DEの交点T、BC-EFの交点R、CD-FAの交点Ｑが一直線上にあることを示している。
